无旋Treap
定义一下变量:
1
2
3
4
5
6
7
8
9
struct Node {
int ls;//每个点的左儿子
int rs;//每个点的右儿子
int val;//每个点的权值
int rnd;//每个点的随机权值
int siz;//以每个点为根的树的大小
} tree[MAXN];
int root;//根节点编号
int tot;//节点总数
1 | struct Node { |
主要有两个核心操作:split(int rt, int &a, int &b, int k) 和 merge(int a, int b, int &rt) ,分别表示将一颗 按权值分裂成两颗 和 以及将两颗 合并。
基本操作
分裂
split(int rt, int &a, int &b, int val)
递归处理,设当前节点为 ,要按值 分裂成两颗树 和 。
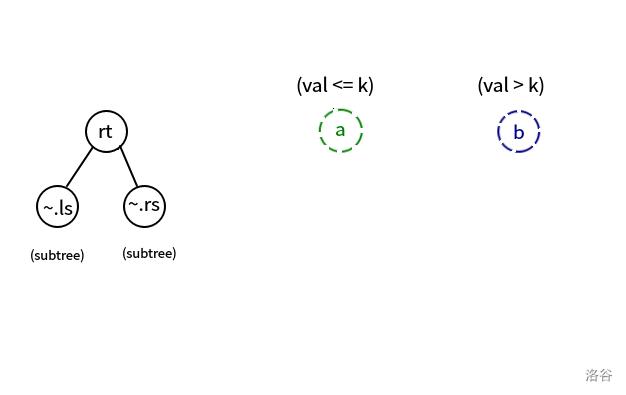
若 ,则 以及它的左子树都可以并入 节点,下一步要将 分裂,如下图。
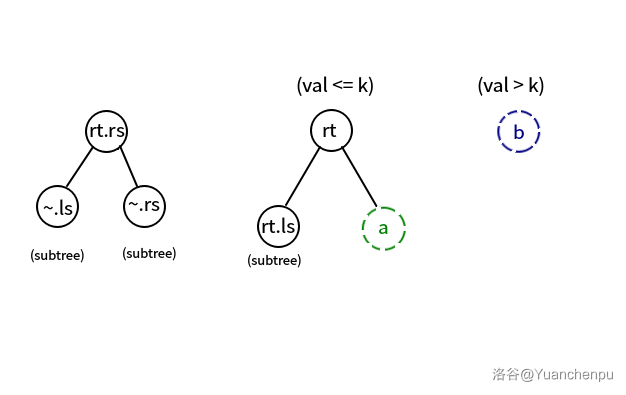
若 ,则 以及它的右子树都可以并入 节点,下一步要将 分裂,如下图。
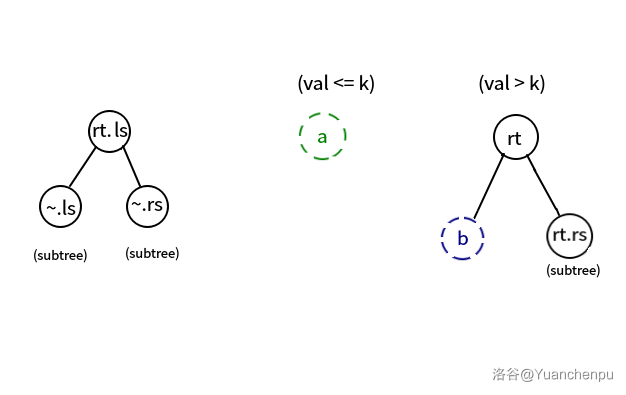
如果 即达到了递归边界,这时候要怎么办呢?
赋值 a = b = 0; 表示当前 , 均为空节点,即上图的绿色和蓝色节点都为空。因为调用函数时是引用的变量,因此 , 的改变也会影响到上级的节点的左儿子或者右儿子。
代码:
1 | void split_by_val(int rt, int &a, int &b, int val) { |
排名分裂是类似的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void split_by_rank(int rt, int &a, int &b, int rank) {
if (rt == 0) {
a = b = 0;
return;
}
int ls = p[rt].ls, rs = p[rt].rs;
if (p[ls].siz + 1 <= rank) {
a = rt;
split_by_rank(rs, p[a].rs, b, rank - p[ls].siz - 1);
} else {
b = rt;
split_by_rank(ls, a, p[b].ls, rank);
}
pushup(rt);
}
1 | void split_by_rank(int rt, int &a, int &b, int rank) { |
合并
操作:merge(a, b, rt):将 , 合并至 ,( 有 )。
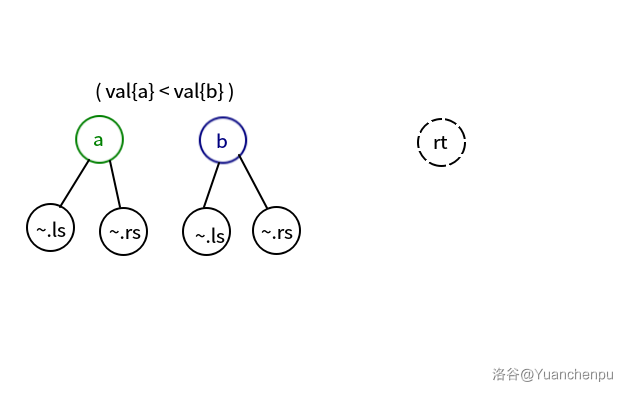
由于要满足堆性质,所以要分情况考虑。
若 则将 和它的左子树复制到 上,赋值 rt = a ,继续递归 merge(a.rs, b, rt.rs)。
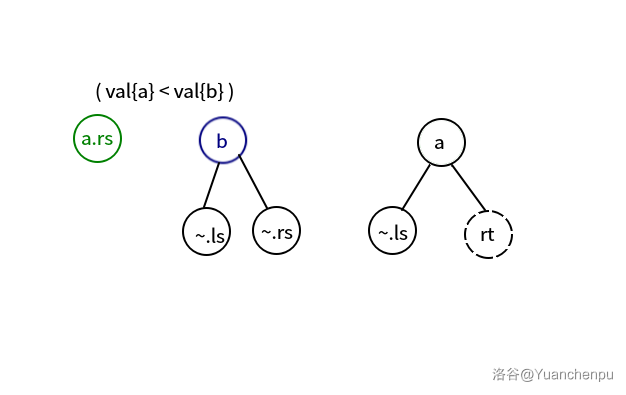
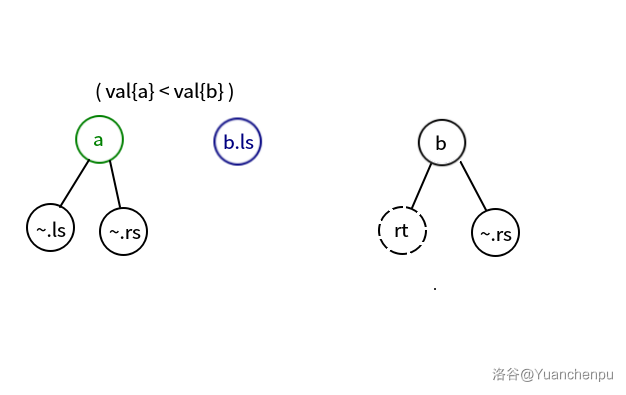
反之,则将 和它的右子树复制到 上,赋值 rt = b ,继续递归 merge(a, b.ls, rt.ls)。
代码
1 | void merge(int a, int b, int &rt) { |
其他操作
插入 insert(a)
将树按权值 分裂成两颗树 和 ,然后新建一个节点 合并 与 至 ,合并 和 至
代码
1 | void insert(int &rt, int val) { |
删除一个权值为 的节点 del(v)
将树 按权值 分裂为 和 。
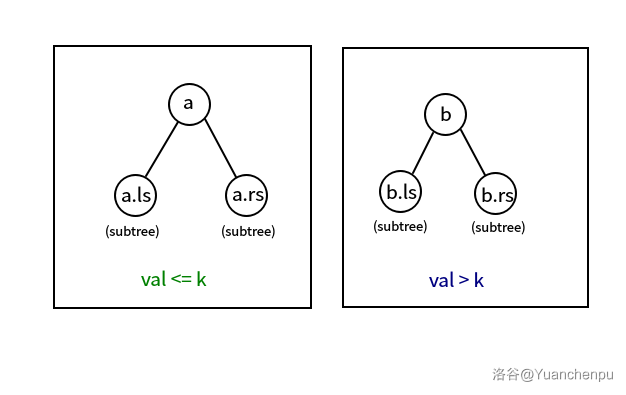
再将 按权值 分裂成 和 。
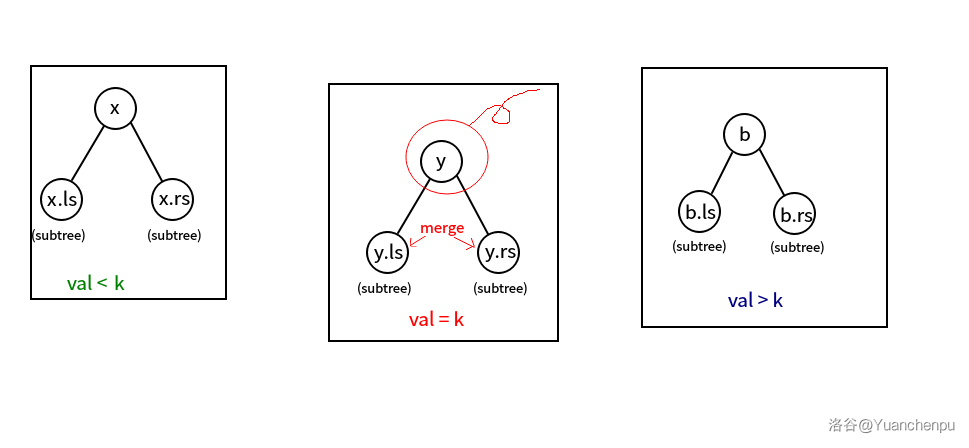
接着,merge(y.ls, y.rs, y) ,表示去掉一个 树中的节点,形成的新的树的根节点仍然是 ,再 merge(x, y, a),merge(a, b, root),重新把几颗树合并到根节点。
代码
1 | void del(int &rt, int val) { |
删除所有权值为 的节点 multidel(v)
与上面类似,最后一步直接 merge(x, b, root) 。
代码
1 | void multidel(int &rt, int val) { |
排名 getrank(rt, v)
直接按照 的权值把树 分开为 和 ,那么 树中最大的应该小于等于 ,那么 的排名就是。
代码:
1 | int getrank(int &rt, int val) { |
查询 小值 getval(rt, k)
记当前节点的左子树大小为 。
,那么 就是答案。
,递归查找左子树的 小值
,递归查找右子树的 小值
代码
1 | int getval(int rt, int k) { |
前驱 getprev(v)
因为要小于 ,所以我们还是按照 的权值划分 ,现在 中最大的数一定小于等于 ,所以我们直接输出 中最大的数就好
代码
1 | int getprev(int &rt, int val) { |
后继 getnext(v)
按照 的权值划分 和 ,现在 中最小的数一定大于 输出 中最小的数。
代码
1 | int getnext(int &rt, int val) { |
扩展内容
持久化:link
水掉splay:link


